Резонанс напряжений и резонанс токов
В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.
Резонанс напряжений
Резонанс напряжений возникает в последовательной RLC-цепи.

Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=wр, а следовательно и индуктивного и емкостного сопротивлений xL=xC. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке UL и на конденсаторе UC будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.
При резонансе напряжения UC и UL могут быть намного больше, чем напряжение источника, что опасно для цепи.

С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.

Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту

Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.
Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.
Резонанс токов
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.

Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.

Выразим резонансную частоту
 Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.
Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.
Резонанс в цепи переменного тока
Урок 14. Физика 11 класс ФГОС


В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности



Конспект урока “Резонанс в цепи переменного тока”
Давайте с вами вспомним, что вывести закон Ома для участка цепи переменного тока, содержащего резистор, катушку индуктивности, конденсатор и источник переменного напряжения нам помогла векторная диаграмма амплитуд напряжений на резисторе, конденсаторе и катушке.
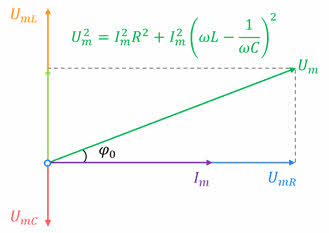
Мы показали, что амплитуда приложенного напряжения должна быть равна геометрической сумме этих амплитуд. Угол между амплитудами приложенного напряжения и силы тока определяет разность фаз между силой тока и напряжением. Тангенс этого угла, как видно из рисунка, равен отношению разности амплитуд напряжений на катушке и конденсаторе к амплитуде напряжения на активном сопротивлении:
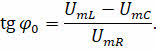
Используя закон Ома для участка цепи нетрудно показать, что этот же угол определяется отношением реактивного сопротивления к активному:
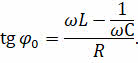
А средняя мощность, выделяемая в цепи на активном сопротивлении, будет определяться выражением, представленном на экране:
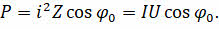
Здесь cos φ — это коэффициент мощности. Являясь безразмерной физической величиной, он характеризует потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей, и показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Из последних двух формул следует, что если реактивное сопротивление цепи равно нулю, то уравнение для мощности примет привычный для нас вид:
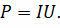
В этом случае в цепи выделяется максимальная мощность — наступает явление резонанса.
Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний силы тока или напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура:
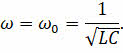
Рассмотрим это явление более подробно. Для начала представим себе, что мы раскачиваем маятник, действуя на него периодически изменяющейся силой. В этом случае маятник будет совершать колебания не самостоятельно, не свободно, а под действием периодической внешней силы. Такие колебания маятника, как мы помним, называются вынужденными колебаниями.
В электрических колебательных контурах также могут происходить вынужденные электромагнитные колебания. Если в каком-либо колебательном контуре, состоящем из катушки индуктивности и конденсатора, всё время действует генератор переменного тока, то ЭДС генератора будет вызывать в этом контуре переменный электрический ток, частота которого будет равна частоте колебаний ЭДС генератора.

Частота этих вынужденных колебаний в общем случае не совпадает с частотой собственных колебании контура:
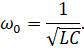
Когда собственная частота колебательного контура далека от частоты ЭДС, действующей в контуре, общее сопротивление контура велико и ток в нём незначителен. Однако если в такой цепи подобрать ёмкость конденсатора и индуктивность катушки так, чтобы их сопротивления оказались равными, то разность фаз между колебаниями силы тока и напряжения станет равным нулю, то есть изменения тока и напряжения будут происходить синфазно:
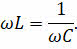
Таким образом, условием возникновения резонанса в колебательном контуре является равенство частоты внешнего подаваемого на контур напряжения частоте собственных колебаний контура:
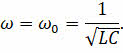
Эту частоту называют резонансной.
При этом условии полное сопротивление контура становится наименьшим и равным активному сопротивлению, а амплитуда силы тока при данном напряжении принимает наибольшее значение. В этом случае амплитуда напряжения на активном сопротивлении равна амплитуде внешнего напряжения, приложенного к участку цепи (Ur = U), а напряжения на катушке индуктивности и конденсаторе одинаковы по модулю и противоположны по фазе:
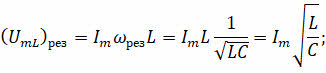
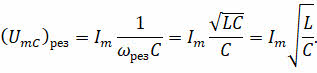
Обратите внимание на то, что амплитудные значения резонансных напряжений на катушке и конденсаторе равны между собой, и они могут значительно превышать амплитуду приложенного напряжения:
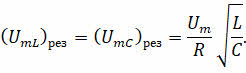
Это явление называется резонансом напряжений. При этом чем меньше активное сопротивление контура, тем сильнее ток в контуре и круче резонансная кривая. Такой случай принято называть острым резонансом.
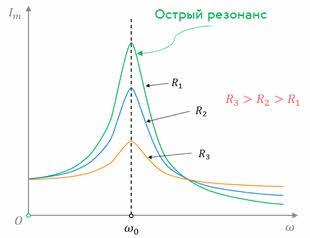
Контур, обладающим острым резонансом, очень чувствителен к колебаниям резонансной частоты. Это широко используется в радио- и электротехнике для усиления колебаний напряжения какой-либо определённой частоты.
Так, например, радиоволны от различных передающих станций возбуждают в антенне радиоприёмника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно связан колебательный контур, в катушке которого возникают вынужденные колебания силы тока и напряжения. Но только при резонансе из колебаний различных частот, возбуждаемых в антенне, контур выделяет только те, частота которых равна его собственной частоте. Настройка контура на нужную частоту обычно осуществляется путём изменения ёмкости конденсатора.
Теперь давайте рассмотрим участок цепи переменного тока, содержащий параллельно включённые конденсатор и катушку индуктивности.

Предположим, что активное сопротивление цепи настолько мало, что им можно пренебречь. Пусть к данной цепи приложено переменное напряжение, изменяющееся по закону синуса:
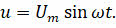
Тогда ток, проходящей в ветви с ёмкостным сопротивлением, будет опережать по фазе приложенное напряжение на π/2. А проходящей в ветви с индуктивным сопротивлением — отставать по фазе на π/2 от приложенного напряжения:
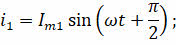
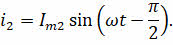
Таким образом, разность фаз токов в двух ветвях равна π, то есть колебания токов в ветвях противоположны по фазе. Амплитуда же тока во внешней цепи равна модулю разности амплитуд сил токов обеих ветвей:
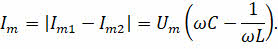
Если частота колебаний в контуре будет равна резонансной частоте, то амплитудные значения сил токов в ветвях будут равны, и амплитуда силы тока во внешней цепи станет равной нулю.
Конечно же, если учесть наличие активного сопротивления, то разность фаз не будет равна π, как и не будет равно нулю амплитудное значение силы тока во внешней цепи. Но оно примет наименьшее возможное значение. При этом амплитуды сил токов в ветвях могут значительно превышать амплитуду тока во внешней цепи.
Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включённые конденсатор и катушку индуктивности, при приближении частоты приложенного напряжения к резонансной частоте называется резонансом токов (или параллельным резонансом).
Это явление используется в резонансных усилителях, позволяющих выделять одно определённое колебание из сигнала сложной формы, а также в индукционных печах, чтобы сила тока в подводящих проводах была гораздо меньше силы тока в катушке.
Для закрепления нового материала давайте решим с вами такую задачу. Контур, состоящий из конденсатора ёмкостью 507 мкФ, катушки индуктивностью 20 мГн и резистора сопротивлением 100 Ом включили последовательно в сеть переменного тока с частотой 50 Гц и напряжением 220 В. Определите силу тока в цепи, сдвиг фаз между напряжением и силой тока, а также резонансную частоту контура.
Резонанс переменного электрического тока
Знание физики и теории этой науки напрямую связано с ведением домашнего хозяйства, ремонтом, строительство и машиностроением. Предлагаем рассмотреть, что такое резонанс токов и напряжений в последовательном контуре RLC, какое основное условие его образования, а также расчет.
Что такое резонанс?
Определение явления по ТОЭ: электрический резонанс происходит в электрической цепи при определенной резонансной частоте, когда некоторые части сопротивлений или проводимостей элементов схемы компенсируют друг друга. В некоторых схемах это происходит, когда импеданс между входом и выходом схемы почти равен нулю, и функция передачи сигнала близка к единице. При этом очень важна добротность данного контура.
 Соединение двух ветвей при резонансе
Соединение двух ветвей при резонансе
Признаки резонанса:
- Составляющие реактивных ветвей тока равны между собой IPC = IPL, противофаза образовывается только при равенстве чистой активной энергии на входе;
- Ток в отдельных ветках, превышает весь ток определенной цепи, при этом ветви совпадают по фазе.
Иными словами, резонанс в цепи переменного тока подразумевает специальную частоту, и определяется значениями сопротивления, емкости и индуктивности. Существует два типа резонанса токов:
- Последовательный;
- Параллельный.
Для последовательного резонанса условие является простым и характеризуется минимальным сопротивлением и нулевой фазе, он используется в реактивных схемах, также его применяет разветвленная цепь. Параллельный резонанс или понятие RLC-контура происходит, когда индуктивные и емкостные данные равны по величине, но компенсируют друг друга, так как они находятся под углом 180 градусов друг от друга. Это соединение должно быть постоянно равным указанной величине. Он получил более широкое практическое применение. Резкий минимум импеданса, который ему свойствен, является полезным для многих электрических бытовых приборов. Резкость минимума зависит от величины сопротивления.
Схема RLC (или контур) является электрической схемой, которая состоит из резистора, катушки индуктивности, и конденсатора, соединенных последовательно или параллельно. Параллельный колебательный контур RLC получил свое название из-за аббревиатуры физических величин, представляющих собой соответственно сопротивление, индуктивность и емкость. Схема образует гармонический осциллятор для тока. Любое колебание индуцированного в цепи тока, затухает с течением времени, если движение направленных частиц, прекращается источником. Этот эффект резистора называется затуханием. Наличие сопротивления также уменьшает пиковую резонансную частоту. Некоторые сопротивление являются неизбежными в реальных схемах, даже если резистор не включен в схему.
Применение
Практически вся силовая электротехника использует именно такой колебательный контур, скажем, силовой трансформатор. Также схема необходима для настройки работы телевизора, емкостного генератора, сварочного аппарата, радиоприемника, её применяет технология «согласование» антенн телевещания, где нужно выбрать узкий диапазон частот некоторых используемых волн. Схема RLC может быть использована в качестве полосового, режекторного фильтра, для датчиков для распределения нижних или верхних частот.
Резонанс даже использует эстетическая медицина (микротоковая терапия), и биорезонансная диагностика.
Принцип резонанса токов
Мы можем сделать резонансную или колебательную схему в собственной частоте, скажем, для питания конденсатора, как демонстрирует следующая диаграмма:
 Схема для питания конденсатора
Схема для питания конденсатора
Переключатель будет отвечать за направление колебаний.
 Схема: переключатель резонансной схемы
Схема: переключатель резонансной схемы
Конденсатор сохраняет весь ток в тот момент, когда время = 0. Колебания в цепи измеряются при помощи амперметров.
 Схема: ток в резонансной схеме равен нулю
Схема: ток в резонансной схеме равен нулю
Направленные частицы перемещаются в правую сторону. Катушка индуктивности принимает ток из конденсатора.
Когда полярность схемы приобретает первоначальный вид, ток снова возвращается в теплообменный аппарат.
Теперь направленная энергия снова переходит в конденсатор, и круг повторяется опять.
В реальных схемах смешанной цепи всегда есть некоторое сопротивление, которое заставляет амплитуду направленных частиц расти меньше с каждым кругом. После нескольких смен полярности пластин, ток снижается до 0. Данный процесс называется синусоидальным затухающим волновым сигналом. Как быстро происходит этот процесс, зависит от сопротивления в цепи. Но при этом сопротивление не изменяет частоту синусоидальной волны. Если сопротивление достаточно высокой, ток не будет колебаться вообще.
Обозначение переменного тока означает, что выходя из блока питания, энергия колеблется с определенной частотой. Увеличение сопротивления способствует к снижению максимального размера текущей амплитуды, но это не приводит к изменению частоты резонанса (резонансной). Зато может образоваться вихретоковый процесс. После его возникновения в сетях возможны перебои.
Расчет резонансного контура
Нужно отметить, что это явление требует весьма тщательного расчета, особенно, если используется параллельное соединение. Для того чтобы в технике не возникали помехи, нужно использовать различные формулы. Они же Вам пригодятся для решения любой задачи по физике из соответствующего раздела.
Очень важно знать, значение мощности в цепи. Средняя мощность, рассеиваемая в резонансном контуре, может быть выражена в терминах среднеквадратичного напряжения и тока следующим образом:
R ср= I 2 конт * R = (V 2 конт / Z 2 ) * R.
При этом, помните, что коэффициент мощности при резонансе равен cos φ = 1
Сама же формула резонанса имеет следующий вид:
Нулевой импеданс в резонансе определяется при помощи такой формулы:
Резонансная частота колебаний может быть аппроксимирована следующим образом:
Как правило, схема не будет колебаться, если сопротивление (R) не является достаточно низким, чтобы удовлетворять следующим требованиям:
Для получения точных данных, нужно стараться не округлять полученные значения вследствие расчетов. Многие физики рекомендуют использовать метод, под названием векторная диаграмма активных токов. При правильном расчете и настройке приборов, у Вас получится хорошая экономия переменного тока.
Резонанс в электрической цепи

Разберемся сначала с важными понятиями.
Колебания внешнего воздействия могут усиливать даже незначительные колебания системы. Наибольший резонанс достигается при совпадении частоты колебаний внешнего воздействия с колебаниями системы.
Одним из примеров явления резонанса, есть расшатывание моста ротой солдат. Это происходит, когда частота шагов солдат, которая являются внешним воздействием, совпадает с частотой колебаний моста. Если возникнет такой резонанс, это может разрушить мост. Именно поэтому солдаты не переходят мосты стройным шагом, а идут в вольном режиме.
Часто встречаемым явлением в физике есть электрический резонанс. Без него невозможно было бы провести телетрансляцию, многие медицинские обследования и прочие важные процессы.
Востребованными резонансами в электрической цепи есть:
- резонанс напряжений;
- резонанс токов.
Резонанс в электрической цепи
Схема (RLC) – это электрическая цепь с последовательными, параллельными или комбинированными соединениями компонентов (резисторами, индукционными катушками и конденсаторами). (RLC) – это сочетание сопротивления, индуктивности и емкости.
Векторная диаграмма в случае последовательного соединения (RLC) -цепи бывает емкостной, активной или индуктивной.
В индуктивной векторной диаграмме резонанс напряжений появляется лишь при нулевом сдвиге фаз и совпадении сопротивлений индукции и емкости.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Резонанс токов через реактивные элементы
Резонанс токов возникает при параллельном соединении реактивных сопротивлений с одинаковыми характеристиками в цепях с переменным током. Во время резонанса токов реактивная индуктивная проводимость приравнивается к реактивной емкостной проводимости, то есть (BL=BC.)
Колебания контура с определенной частотой совпадают с частотой колебаний источника.
Простейшим примером цепи, в которой может произойти резонанс токов, есть параллельное соединение катушки с конденсатором.
Поскольку реактивные сопротивления совпадают по модулю, то амплитуды токов конденсатора и катушки также будут совпадать и могут достичь наибольшего значения амплитуды. Согласно первому закону Кирхгофа (IR) равняется току источника. Иначе говоря, ток проходит лишь через резистор. Если рассмотреть параллельный контур (LC,) то при частоте резонанса его сопротивление будет огромным. В условиях режима гармонии при частоте резонанса в контуре будет расход тока лишь для восполнения потерь на активном сопротивлении.
Значит, в последовательной цепи (RLC) импеданс наименьший при частоте резонанса и равняется активному сопротивлению контура, при этом в параллельной цепи (RLC) импеданс наибольший при частоте резонанса и равняется сопротивлению утечки, что фактически есть активным сопротивлением контура. Это значит, что для обеспечения резонанса силы тока или напряжения в цепи необходима ее проверка с целью определения суммарного сопротивления и проводимости. Кроме того, ее мнимая часть должна равняться нулю.
Резонанс напряжений
Резонанс напряжений имеет место в цепи переменного тока в случае последовательного соединения активного (R) , емкостного (C) и индуктивного (L) компонентов. Резонанс напряжений состоит в совпадении внутренних колебаний источника и внешних колебаний контура. Резонанс напряжений применяется с пользой, но бывает и опасен. Например, данное явление применяют в радиотехнике, а опасность его состоит в том, что при резких скачках напряжения может произойти поломка оборудования и даже его возгорание.
Резонанс напряжения достигают несколькими путями:
- подбирая индуктивность катушки;
- подбирая емкость конденсатора;
- подбирая угловую частоту (ω_0) .
Эти величины подбирают с помощью таких формул:
Частота (ω_0) – это резонансная величина. При постоянных напряжении и активном сопротивлении в цепи сила тока в процессе резонанса напряжения наибольшая и равняется отношению напряжения к активному сопротивлению. То есть, сила тока полностью не зависима от реактивного сопротивления. Если реактивные сопротивления индукции и емкости одинаковы и по своей величине превышают активное сопротивление, тогда на зажимах катушки и конденсатора будет напряжение, сильно превышающее напряжение на зажимах контура.
Не нашли что искали?
Просто напиши и мы поможем
Кратность превышения напряжения на зажимах катушки и конденсатора в соотношении с напряжением контура рассчитывается так:
Величина (Q) является добротностью контура и описывает его резонансные характеристики.
Величина, обратная добротности контура, – это затухание контура ( <1 over Q>) .
Явление резонанса на практике
Электрический резонансный трансформатор, который был разработан Николой Теслой в конце XIX века, является ярким примером практического применения резонанса в электрических цепях. Тесла проводил массу экспериментов при разных конфигурациях резонансных цепей.
На сегодняшний день словосочетанием «катушка Теслы» называют высоковольтные резонансные трансформаторы. Такие приспособления применяют для генерации высокого напряжения и частоты переменного тока. Если простые трансформаторы используют для передачи энергии с первичной на вторичную катушку, то резонансные – для хранения электрической энергии во временном режиме.
При помощи данного приспособления, посредством управления воздушным сердечником резонансно настроенного трансформатора, при незначительной силе тока получают высокие напряжения. При этом у каждой катушки есть собственная емкость и она работает как резонансный контур. Для создания еще большего напряжения достигают резонанса двух контуров.
Резонанс напряжений
Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.
Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.
Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.
Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС.
Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:
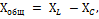
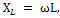
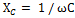
Применив к этой цепи закон Ома, получим:
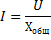
Формулу эту можно преобразовать следующим образом:
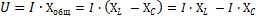
В полученном равенстве I XL — действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а I ХС — действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.
Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.
Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:
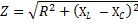
где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать:
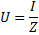

Резонанс напряжений в цепи переменного тока
Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.
Иначе говоря, от одновременного действия этих двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.
Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда XL = ХС или, что то же, когда ω L = 1 / ωС.
Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома I = U / R , где вместо Z теперь поставлено R.
Одновременно с этим действующие напряжения как на катушке UL = I XL так и на конденсаторе Uc = I ХС окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений .
На рис. 1 приведены кривые напряжений, тока и мощности при резонансе напряжений в цепи.
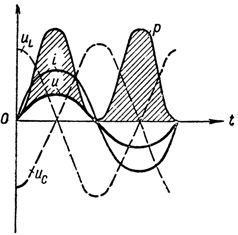
График тока напряжений и мощности при резонансе напряжений
Следует твердо помнить, что сопротивления XL и ХС являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как XL = ω L возрастет, а ХС = = 1 / ωС уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
Действительно, в цепи с одной катушкой индуктивности происходит колебание энергии, т. е. периодический переход энергии из генератора в магнитное поле катушки. В цепи с конденсатором происходит то же самое, но за счет энергии электрического поля конденсатора. В цепи же с конденсатором и катушкой индуктивности при резонансе напряжений (XL = ХС) энергия, раз запасенная цепью, периодически переходит из катушки в конденсатор и обратно и на долю источника тока выпадает только расход энергии, необходимый для преодоления активного сопротивления цепи. Таким образом, обмен энергии происходит между конденсатором и катушкой почти без участия генератора.
Стоит только нарушить резонанс напряжений в цени, как энергия магнитного поля катушки станет не равной энергии электрического поля конденсатора, и в процессе обмена энергии между этими полями появится избыток энергии, который периодически будет то поступать из источника в цепь, то возвращаться ему обратно цепью.
Явление это очень сходно с тем, что происходит в часовом механизме. Маятник часов мог бы непрерывно колебаться и без помощи пружины (или груза в часах-ходиках), если бы не силы трения, тормозящие его движение.
Пружина же, сообщая маятнику в нужный момент часть своей энергии, помогает ему преодолеть силы трения, чем и достигается непрерывность колебаний.
Подобно этому и в электрической цепи, при явлении резонанса в ней, источник тока расходует свою энергию только на преодоление активного сопротивления цепи, тем самым поддерживая в ней колебательный процесс.
Итак, мы приходим к выводу, что цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях XL = ХС превращается в колебательную систему . Такая цепь получила название колебательного контура.
Из равенства XL = ХС можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:
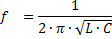
Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений :
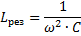
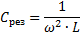
Таким образом, изменяя любую из этих трех величин ( f рез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур.
Пример полезного применения резонанса напряжений : входной контур приемника настраивается конденсатором переменной емкости (или вариометром) таким образом, что в нем возникает резонанс напряжений. Этим достигается необходимое для нормальной работы приемника большое повышение напряжения на катушке по сравнению с напряжением в цепи, созданным антенной.
Наряду с полезным использованием явления резонанса напряжений в электротехнике технике часто бывают случаи, когда резонанс напряжений вреден. Большое повышение напряжения на отдельных участках цепи (на катушке или на конденсаторе) по сравнению с напряжением генератора может привести к порче отдельных деталей и измерительных приборов.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Как возникает резонанс напряжения и токов: в чем опасность явления, как его можно использовать

Это явление можно наблюдать в индуктивных ёмкостных цепях. Резонанс широко используют в радиотехнике для наведения приёмника на определённую частоту.
У этого явления есть и отрицательная сторона – может повредить электрические приборы и кабели.
По сути, резонанс токов — это совмещение частоты разных систем. Давайте выясним, что это за явление, какова его значимость, в каких областях применяется.
Индуктивность, ёмкость и их реактивная сопротивляемость

Индуктивность – это свойство объекта копить энергию в намагниченном поле. Характеризуется тем, что фазный ток отстаёт от напряжения. Устройства индуктивности – это электрические моторы, трансформаторы.
Ёмкость – элементы, обладающие способностью копить энергию при помощи электрополя.
Характеризуются отставанием величины напряжения от величины тока. Это варикапы, различные конденсаторы. Это их главные свойства, детали в рамках данной статьи не учитываются.
Помимо названых элементов есть и другие, которые обладают определённой индуктивностью и ёмкостью.
Индуктивность и ёмкость в цепи тока переменной величины

Ёмкость в линии с током постоянной величины выглядит как разомкнутый отрезок цепи, индукция представлена проводником. При переменном токе реактивный резисторный аналог представлен катушками с устройствами конденсации.
Реактивная сопротивляемость зависима от значения ёмкости либо индуктивности, а также частоты тока с переменной величиной.
Глядя на расчёт реактивного значения, становится заметно, что имея определённые значения индуктивного либо ёмкостного элемента, разность их равняется нулю, и, как следствие, в остатке будет находиться активное сопротивление. У этой ситуации есть ещё некоторые нюансы.
Резонанс напряжения

Это явление возникнет, когда к генератору последовательно подключить катушку с конденсатором с одинаковыми реактивными сопротивлениями.
Обращаем ваше внимание, что ситуации, когда реактивными бывают только ёмкость и индуктивность, существуют только в идеале. А в реальности всегда есть сопротивление проводов, хотя и незначительное.
При резонансном эффекте конденсатор с дросселем обмениваются энергией. При запуске генератора, конденсатор начинает накапливать энергию, а затем, после выключения, в результате обмена начинают происходить колебания.
Схема, включающая в себя ёмкость и индуктивность, называется колебательным контуром.
Периодичность вычисляется формулой Томпсона:

Поскольку сопротивление зависимо от частоты, соответственно, при увеличении частоты сопротивляемость индуктивности возрастает, при этом у ёмкости, наоборот, снижается.
Общий показатель сопротивления будет ощутимо понижаться, когда сопротивления одинаковые.
К главным показателям контура относятся частота и передаточный коэффициент. Если разобрать контур с четырьмя полюсами, становится понятно, что передаточный коэффициент равен добротности (Q).
В резонансе, чем значительнейпоказатель добротности, тем значительней напряжение на контурных элементах по сравнению с напряжением на генераторе.
В контуре показатели мощности падают из-за сопротивления. Энергия поставщика используется лишь для поддержки колебаний.
Токовый резонанс

Это явление происходит при параллельном подключении ёмкости с индуктивностью.
Работает это по следующей схеме: ток большого значения проходит между катушкой и конденсаторным устройством, когда в части цепи без разветвления ток нулевой.
Это обуславливается возросшим сопротивлением при получении частоты резонанса. Проще говоря, в резонансной точке суммарное сопротивление достигает максимума. В результате роста или падения частоты одно сопротивление растёт, второе падает.
Обобщая, можно сказать, что всё происходит по аналогии с вышеупомянутым процессом, причины появления токового резонанса заключаются в следующем:
- Частотность питания равна резонансной частоте в контуре.
- Проводимость тока переменного значения одинаковы, что у ёмкости, что у индукции.
Практическое применение напряжения
Давайте разберём полезные и вредные свойства данного явления.
Несомненную пользу эффект резонанса напряжения принёс в радиоэлектронике. В цепи радиоприёмника вмонтирована катушка с конденсаторным устройством, соединённые с антенной.
Движением сердечника, меняя индукцию, либо ёмкостную величину с помощью конденсатора, подбирается частота резонанса. Вследствие этого напряжение катушки растёт, и радиоприёмник фиксирует определённую волну.
Но для кабелей такое явление довольно опасно, так как при подаче напряжения на кабель, не имеющий нагрузки, есть вероятность прострела изоляционной оболочки. Чтобы этого не произошло, подсоединяют балластную нагрузку.
Такая же ситуация ведёт к поломке частей электроники, приборов контроля и измерений и прочего электрического оборудования.
Резонансное явление напряжения – вещь достаточно интересная и заслуживает внимания. Резонанс возможен только в индуктивных ёмкостных цепях. В линиях, где активное сопротивление велико, это явление невозможно.
Подведём итог, коротко дав ответы по данной теме:
- Где возможно возникновение резонанса?
Ответ: в индуктивных ёмкостных схемах.
- При каких условиях?
Ответ: реактивные сопротивления должны быть равны.
- Как ликвидировать резонанс?
Ответ: Поменять частоту, добавить активное сопротивление.
Надеемся, теперь вам понятно, что это за явление, условия для его появления и практическое использование.
Соединение резисторов
Время на чтение:
Резистор — это прибор, который обладает устойчивым, стабильным показателем сопротивления. Это помогает производить регулировку параметров на любом участке схемы. В этой статье говорится о том, как подключить резистор в цепь и какие методы для этого существуют. Также продемонстрированы несколько простых, но полезных схем, которые могут пригодиться при работе с электрикой.
Что такое соединение резисторов
Подключение приборов различными методами помогает получить нужное число мощности одной единицы цепи. Есть три основных метода подключения прибора — последовательное, параллельное и смешанное. Ниже подробно рассказано о каждом из них.
 Как выглядят резисторы
Как выглядят резисторы
Внимание! Для работы необходимо использовать только качественные приборы, на которые действует гарантия.
Как подключить резистор в цепь
Для сборки составного устройства необходимо соединить несколько элементов одним из основных методов и таким образом получить нужный номинальный показатель. В практике это используется очень часто. Навыки правильного подключения устройств и расчета их общего сопротивления используются мастерами для ремонта проводки или радиолюбителями при сборке устройства. В интернете можно найти много схем с различным видом подключения. Ниже описано какое соединение резисторов называется параллельным.
 Параллельное соединение резисторов схема
Параллельное соединение резисторов схема
Параллельно
Параллельное — это одно из двух типов электрических соединений, когда два вывода единственного устройства соединены с соответствующими выводами других элементов. Очень часто их могут соединять последовательно или параллельно, чтобы сделать более усложненные электрические схемы.
При этом виде соединения напряжение на всех устройствах будет равным, а проходящий через них ток — пропорционален их сопротивлению.
Такой вариант подключения один из простых, очень часто именно его рекомендуют использовать тем, кто не имеет опыта работы с электрикой.
Последовательно
Формула расчета достаточно легкая. Общее сопротивление при параллельном соединении формула:
Сопротивление двух и более параллельно соединенных резисторов указано как Rобщ.
 Последовательный способ подключения
Последовательный способ подключения
Остальные элементы указываются как R, R2, R3 и так далее.
Обратите внимание! Используя последовательное соединение, необходимо запомнить один важный нюанс. Из общего количества компонентов, соединённых последовательным методом, основную роль занимает тот, у которого самое высокое сопротивление.
Как это понять? Для примера, если необходимо соединить три устройства, номинал которых будет равняться 1, 10 и 100 Ом, то в итоге получится составной на 111 Ом.
 Смешанный тип подключения
Смешанный тип подключения
Если исключить прибор на 100 Ом, то все сопротивление схемы резко снизится до 11 Ом. А если исключить, например, на 1 Ом, то показатель получится уже 110 Ом. В итоге устройства с небольшим сопротивлениями в последовательной цепочке почти не влияют на все показатели.
Какая мощность тока при последовательном и параллельном соединении
При соединении устройств последовательным методом ток будет проходить через каждое сопротивление. Показатель тока в любом месте цепочки будет равным. Это правило определяется при помощи закона Ома. Если суммировать все показатели в цепи, получится такое выражение:
 Образец цепи
Образец цепи
R = 200+100+51+39 = 390 Ом.
Напряжение на схеме равняется 100 В, по правилу Ома сила тока будет выражаться:
I = U/R = 100/390 = 0,256 A.
Теперь с помощью этих уравнений можно посчитать мощность при последовательном подключении, используя это выражение:
P = I2 x R = 0,2562×390 = 25,55 Вт.
При параллельном соединении все основания нужно подсоединить к одному узлу цепи, а концы — к другому. В таком варианте получается разветвление тока, и он будет проходить по каждому узлу. По правилу Ома, сила тока будет обратно пропорциональна всем имеющимся устройствам, а показатель напряжения везде одинаковый.
При смешанном подключении используются свойства обоих видов соединений.
 Закон Ома для участка цепи
Закон Ома для участка цепи
Как правильно рассчитать сопротивление
Для выбора и установки элементов в цепь нужно заранее просчитать номинал и мощность составных частей.
Применяют для этого правило Ома для участка цепи, чтобы рассчитать сопротивление, выражение выглядит так:
U — будет напряжением на выводах компонента.
I — показатель тока на участке цепи.
Это выражение используется для токов постоянного направления.
Если трудно самостоятельно рассчитать этот показатель, то существуют специальные онлайн-калькуляторы. Туда необходимо вставить имеющиеся значения и можно получить результат за секунды. Но поскольку закон Ома изучается еще в школе, то не составит проблем провести вычисления самостоятельно.
Внимание! Если нет опыта в работе с электрикой, желательно не выполнять ремонт проводки самостоятельно, потому что при неправильной работе может случиться короткое замыкание, что чревато возникновением пожара. Также необходимо помнить, что при работе с проводкой нужно полностью обесточить сеть.
В заключении необходимо отметить, что подключать резисторы можно тремя способами: параллельно, последовательно и смешанно. Для тех, кто не имеет особых навыков работы с электрикой, рекомендуется выбирать последовательный метод соединения.





